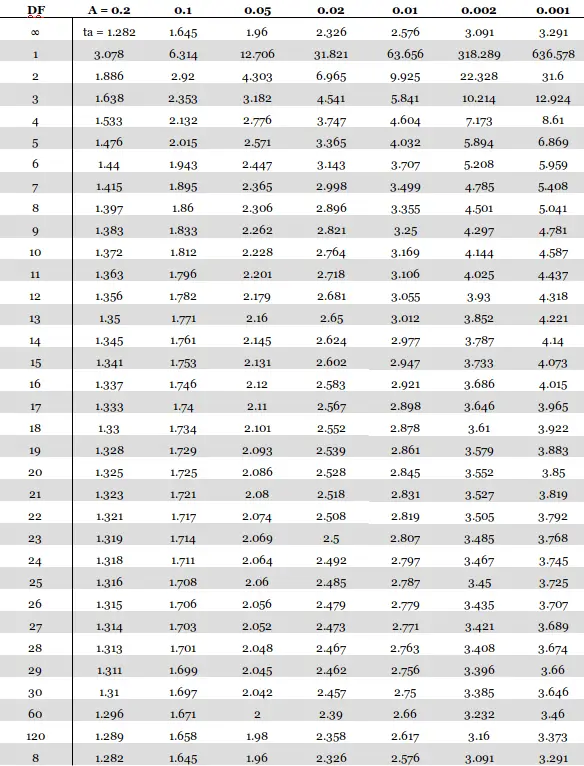
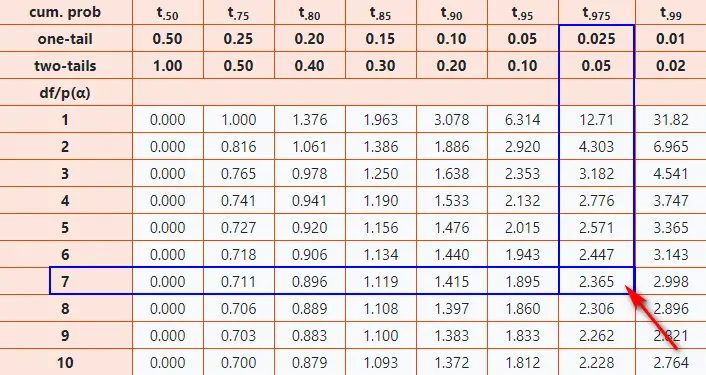
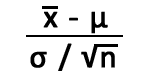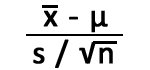T Table - T Distribution (Score, Chart)

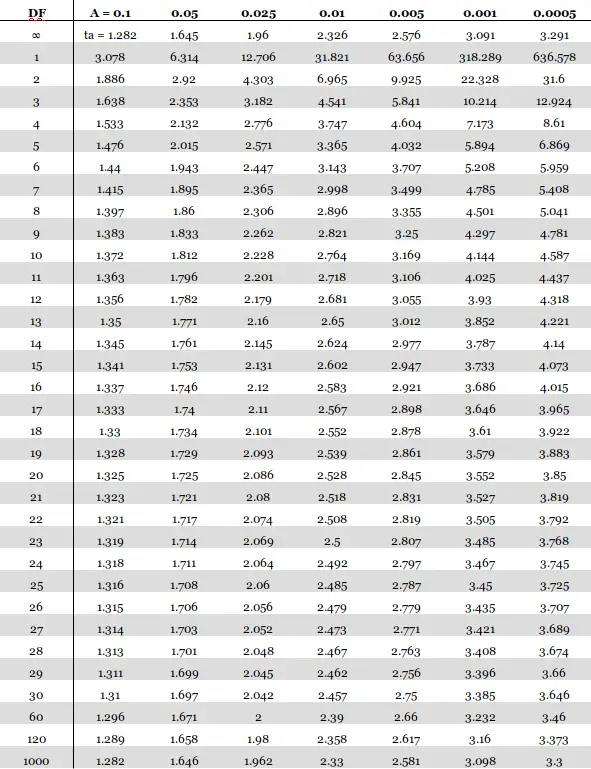
T Table contains the critical values of the T Distribution. The column contains all the T-Distribution probabilities denoted by "Alpha" or "p". The row contains all the degrees of freedom denoted by "df". Also, here you will get one and two tail T score tables or charts online.

cum. prob	t_.50	t_.75	t_.80	t_.85	t_.90	t_.95	t_.975	t_.99	t_.995	t_.999	t_.9995
one-tail	0.50	0.25	0.20	0.15	0.10	0.05	0.025	0.01	0.005	0.001	0.0005
two-tails	1.00	0.50	0.40	0.30	0.20	0.10	0.05	0.02	0.01	0.002	0.001
df/p(α)
1	0.000	1.000	1.376	1.963	3.078	6.314	12.71	31.82	63.66	318.31	636.62
2	0.000	0.816	1.061	1.386	1.886	2.920	4.303	6.965	9.925	22.327	31.599
3	0.000	0.765	0.978	1.250	1.638	2.353	3.182	4.541	5.841	10.215	12.924
4	0.000	0.741	0.941	1.190	1.533	2.132	2.776	3.747	4.604	7.173	8.610
5	0.000	0.727	0.920	1.156	1.476	2.015	2.571	3.365	4.032	5.893	6.869
6	0.000	0.718	0.906	1.134	1.440	1.943	2.447	3.143	3.707	5.208	5.959
7	0.000	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499	4.785	5.408
8	0.000	0.706	0.889	1.108	1.397	1.860	2.306	2.896	3.355	4.501	5.041
9	0.000	0.703	0.883	1.100	1.383	1.833	2.262	2.821	3.250	4.297	4.781
10	0.000	0.700	0.879	1.093	1.372	1.812	2.228	2.764	3.169	4.144	4.587
11	0.000	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106	4.025	4.437
12	0.000	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055	3.930	4.318
13	0.000	0.694	0.870	1.079	1.350	1.771	2.160	2.650	3.012	3.852	4.221
14	0.000	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977	3.787	4.140
15	0.000	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947	3.733	4.073
16	0.000	0.690	0.865	1.071	1.337	1.746	2.120	2.583	2.921	3.686	4.015
17	0.000	0.689	0.863	1.069	1.333	1.740	2.110	2.567	2.898	3.646	3.965
18	0.000	0.688	0.862	1.067	1.330	1.734	2.101	2.552	2.878	3.610	3.922
19	0.000	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861	3.579	3.883
20	0.000	0.687	0.860	1.064	1.325	1.725	2.086	2.528	2.845	3.552	3.850
21	0.000	0.686	0.859	1.063	1.323	1.721	2.080	2.518	2.831	3.527	3.819
22	0.000	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819	3.505	3.792
23	0.000	0.685	0.858	1.060	1.319	1.714	2.069	2.500	2.807	3.485	3.768
24	0.000	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797	3.467	3.745
25	0.000	0.684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.450	3.725
26	0.000	0.684	0.856	1.058	1.315	1.706	2.056	2.479	2.779	3.435	3.707
27	0.000	0.684	0.855	1.057	1.314	1.703	2.052	2.473	2.771	3.421	3.690
28	0.000	0.683	0.855	1.056	1.313	1.701	2.048	2.467	2.763	3.408	3.674
29	0.000	0.683	0.854	1.055	1.311	1.699	2.045	2.462	2.756	3.396	3.659
30	0.000	0.683	0.854	1.055	1.310	1.697	2.042	2.457	2.750	3.385	3.646
40	0.000	0.681	0.851	1.050	1.303	1.684	2.021	2.423	2.704	3.307	3.551
60	0.000	0.679	0.848	1.045	1.296	1.671	2.000	2.390	2.660	3.232	3.460
80	0.000	0.678	0.846	1.043	1.292	1.664	1.990	2.374	2.639	3.195	3.416
100	0.000	0.677	0.845	1.042	1.290	1.660	1.984	2.364	2.626	3.174	3.390
1000	0.000	0.675	0.842	1.037	1.282	1.646	1.962	2.330	2.581	3.098	3.300
Z	0.000	0.674	0.842	1.036	1.282	1.645	1.960	2.326	2.576	3.090	3.291
	0%	50%	60%	70%	80%	90%	95%	98%	99%	99.8%	99.9%
	Confidence Level

T Table PDF

You may also like to see Z Table and ASCII Codes.

Statistical Concept of T Table or T Distribution

Let's understand the concept of T distribution with an example. Suppose a sample space containing n observations from a normally distributed population. Then the Standard Normal Distribution:

Z =

This concept failed in real because we are mostly unaware of the value of population standard deviation (σ). It is a parameter for the standard deviation of the entire population. However, we don't know its value so we can't put it in the formula.

The best solution for the above problem will be to use the Sample Standard Deviation rather than using the Population Standard Deviation.

Therefore, the formula becomes:

T =

Here "s" is the Sample Standard Deviation. The value of "σ" was constant and the value of "s" varies sample to sample. Hence, the Sample Standard Deviation will also vary sample to sample. Consequently, the whole quantity will have different values. Hence, we label this equation as T distribution.

The T distribution has (n - 1) degrees of freedom. When the degrees of freedom rise, the T distribution inclines towards the standard normal distribution.

Also, the z-score or standard normal distribution can be calculated using the Z-Score Calculator.

Types of T Distribution Table

In statistics, you will find two types of T table. The main difference between both the tables is in the number of ends of the distribution of sample statistic. The number of ends is known as tails.

Depending upon the number of tails, there are two types of T Distribution tables:

1. One-tailed T distribution

2. Two-tailed T distribution

How to use the T Score Table?

Till now, we have known about what is T table, its equation, and types. Now, let's learn how to calculate the T-Score from the T Chart. Here I have tried to explain the calculation process. You just need to follow the two simple steps.

Step 1:

Find 'Degrees of Freedom'. The degrees of freedom can be easily estimated using the below formula.

DF = n - 1

Subtracting one from the sample size(n) ultimately gives you the degrees of freedom(DF).

So, if we take the n = 6, then the DF = 6 – 1 = 5.

Step 2:

Now, you have the DF value. The next step is to locate it on the one-tailed or two-tailed charts. Usually, the left-hand side has degrees of freedom. After that, look for the alpha(α) value. The result is at the intersection of row and column of your DF and alpha value respectively.

Still, confused? Let's make it more simple with an example of a T-Distribution calculation. In this example, we will use a one-tailed T-table.

Example

Let's take,

Degree of freedom = 7
Alpha(α) Value = 0.025

Look for the DF = 7 on the left-hand side of the table. Simultaneously, look for alpha(α) value = 0.025 on the top side of the table. You will find that 2.365 is the value present in between this row and column.

Finally, you can use the DF and alpha values to determine the probabilities for T-Distribution values from the T table.